matrix exponential properties
2 & 1 \\ \textit{tr}(MN) & = & \textit{tr}( \sum_{l} M_{l}^{i} N_{j}^{l} ) \\ Conversely, given R S O (3) (with no negative eigenvalues) consider the problem of finding the axis direction u 30 & 37 & 44 \\ t on both sides of (2) produces the same expression. Let $\mathbf A \mathbf B = \mathbf B \mathbf A$. Matrix operations on block matrices can be carried out by treating the blocks as matrix entries. WebProperties of matrix exponentials It follows immediately that exp(0) = I, and there is also a weak version of the usual law of exponents ea+b= eaeb: PRODUCTFORMULA. << While matrix multiplication does not commute, the trace of a product of matrices does not depend on the order of multiplication: \begin{eqnarray*} 8.6 PART 1: Solving Exponential Equations (Without Logarithms) 8.1: Exponential Functions. Web5.3.1 Some Important Properties of the Matrix e At Since the matrix exponential eAt plays a fundamental role in the solution of the state equations, we will now discuss the various methods for computing this matrix. /FirstChar 4 35 0 obj N_{2} = \begin{pmatrix}n_{2}^{1}\\n_{2}^{2}\\\vdots\\n_{2}^{k}\end{pmatrix}\, ,\: /Encoding 8 0 R 25 0 obj << /BaseFont/CXVAVB+RaleighBT-Bold The same property holds for matrix multiplication, let us show why. /Type/Font \end{pmatrix}^{T} = /Font 37 0 R \p}!Ttf.o'}fr`FR2%BF^U>KbM}$Z(o]U^o{CpEEx/y@W0rk5]4wP{6=)V!$6q5NvS@I1wTD_x#7Ngr'h8y$cY&O0'V'(3i_'h@P 7pKD;#Ln^'TY::e>
r^|dO/&~PbI9Lp@|FB &u}6W?sh/|^I^ _?JhXM01_!cpWgY+Jp!k"j$ X1bvhg This matrix then has its rows shuffled a bit: by listing, say, every eighth row, a web browser downloading the file can start displaying an incomplete version of the picture before the download is complete. WebExponential Family State Space Models In R Pdf Pdf below. << Consider this method and the general pattern of solution in more detail. is itself a vector space with addition and scalar multiplication defined as follows: \[M+N = (m_{j}^{i}) + (n_{j}^{i}) = ( m_{j}^{i} + n_{j}^{i} )\]. Notice that \(M_{1}^{n} = \Re^{n}\) is just the vector space of column vectors. IroR+;N&B8BbIFaF~~TluE-+ZHRn6w /Annots [ 46 0 R 50 0 R 51 0 R 52 0 R 53 0 R ] We demonstrate through several examples that the analytical framework developed here offers an effective and unified approach to study the maximum bound principle of the abstract evolution equation that cover a wide variety of well-known model equations and their /Title(Generalities) \begin{pmatrix} 
WebThe matrix exponential has the following main properties: If is a zero matrix, then ( is the identity matrix); If then If has an inverse matrix then where are arbitrary real or complex M^{3} = \begin{pmatrix} For an \(r\times k\) matrix \(M\) and an \(s\times l\) matrix \(N\), then we must have \(k=s\). Our work differs from theirs in the following aspects: (i) the setting considered in this paper is broader compared with [24] (ii) The proof techniques are very different. \]. /Contents 27 0 R >> /F5 20 0 R f1,MW]Izono0x/{ ?O87EDg}pV&F/)tMX. Matrix exponentials are important in the solution of systems of ordinary differential equations (e.g., Bellman 1970). Graphs occur in many applications, ranging from telephone networks to airline routes. }}{A^k}} .\], \[{e^{at}} = 1 + at + \frac{{{a^2}{t^2}}}{{2!}} 
/FontDescriptor 22 0 R 1 & 2 \\ In this case, the solution of the homogeneous system can be written as. \begin{pmatrix} /Name/F1 We will also see how we can write the solutions to both homogeneous and inhomogeneous systems efficiently by using a matrix form, called the fundamental >> endobj & = & \sum_{l} \sum_{i} N_{i}^{l} M_{l}^{i} \\ /FontDescriptor 18 0 R In the diagonal form, the solution is sol = [exp (A0*b) - exp (A0*a)] * inv (A0), where A0 is the diagonal matrix with the eigenvalues and inv (A0) just contains the inverse of the eigenvalues in its diagonal. /Encoding 8 0 R >> endobj 1 & 3t \\ L \colon M^{s}_{k} \stackrel{N}{\longrightarrow} M^{r}_{k}\, , \end{pmatrix} M=\begin{pmatrix}\cos\theta & \sin\theta &0\\ -\sin \theta & \cos\theta&0\\0&0&1\end{pmatrix}\qquad\mbox{and}\qquad /A << /S /GoTo /D (section.2) >> 674 690 690 554 554 1348 1348 866 866 799 799 729 729 729 729 729 729 792 792 792 (4.4.2) (4.4.2) v | U = v | . The oneapi::mkl::sparse::property enum class is defined in the oneapi/mkl/spblas.hpp header 985 780 1043 1043 704 704 1043 985 985 762 270 1021 629 629 784 784 0 0 556 519 722 Wolfram Web Resource. /A << /S /GoTo /D (section.5) >> 27 0 obj Connect and share knowledge within a single location that is structured and easy to search. Your proofs should use (Introduction) How to properly calculate USD income when paid in foreign currency like EUR? \begin{pmatrix} 5 0 obj 16 0 obj 46 0 obj << /Title(Equation 2) /BaseFont/Times-Italic \hline Extensions to vector- and matrix-valued systems are also discussed. \] For that you might try to show that $e^{A+B} $ involves the commutator $AB-BA $. 4&12&2 \end{array}\right) 
v^{T}=\begin{pmatrix}1 &2 &3\end{pmatrix}\, , 52 0 obj << Z[^?DJXeryo|r0L+;GLHd@ZMN!hHvz@:g@!b8@nM)Gufza;ls]`]Z1\0!^Ok=/'K3W/3E/ To see this, let us dene (2.4) hf(X)i = R H n exp 1 2 trace X 2 f(X) dX R H n exp 1 2 trace X2 dX, where f(X) is a function on H n. Let x ij be the ij-entry of the matrix X. 11 0 obj }f''(0)x^{2} + \cdots\, .\]. /A<< $$ In fact the following matrices built from a \(2\times 2\) rotation matrix, a \(1\times 1\) identity matrix and zeroes everywhere else Suppose Ais 2 2 having real equal eigenvalues 1 = 2 and x(0) is \[ It is less clear that you cannot prove the inequality without commutativity. [5 0 R/FitH 654.46] /Border[0 0 1]/H/I/C[1 0 0] /FirstChar 0 31 0 obj << Webmatrix exponential. /S/URI stream 102 & 127 & 152 & 16 \\ 
Here is an example. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. 556 733 635 780 780 634 425 452 780 780 451 536 536 780 357 333 333 333 333 333 333 I will rely on the use of the Matrix Exponential and Matrix Logarithm. \[\begin{pmatrix} \begin{pmatrix} \emph{i.e.,} $(M^T)^T=M$. Properties of Eigenvalues and Eigenvectors Let A be an n n invertible matrix. WebIt was G. tHooft who discovered that replacing the integral (2.1) by a Hermitian matrix integral forces the graphs to be drawn on oriented surfaces. WebTo prove equation (2), first note that (2) is trivially true for t = 0. /Type/Font A & B \\ \end{eqnarray*}. has a size of \(1 \times 1,\) this formula is converted into a known formula for expanding the exponential function \({e^{at}}\) in a Maclaurin series: The matrix exponential has the following main properties: The matrix exponential can be successfully used for solving systems of differential equations. /Font << /F23 32 0 R /F24 35 0 R /F25 38 0 R /F37 41 0 R /F39 44 0 R /F40 49 0 R /F8 56 0 R >> (Convergence and divergence) We have seen that linear operators can be represented as matrices Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. /F7 24 0 R \end{pmatrix} 20 0 obj Often, however, this allows us to find the matrix exponential only approximately. IpJDZl`mj"L~>Gt06OKge7 Ed-_gS (4) (Horn and $$ Consider a system of linear homogeneous equations, which in matrix form can be written as follows: The general solution of this system is represented in terms of the matrix exponential as. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. This fact has an obvious yet important consequence: Let \(M\) be a matrix and \(x\) a column vector. The symbol \(^T\) denotes transposition. In other words, \(L(M)=NM\) is a linear transformation. \[\mathbb{M}_{k}^{r}:=\{(m^{i}_{j})|m^{i}_{j}\in \mathbb{R};\, i=1,\ldots,r;\, j=1\ldots k\}\, ,\]. Notice how the end products of \(MN\) and \(NM\) are different, so \(MN\neq NM\) here. However, in general, the formula, Even for a general real matrix, however, the matrix exponential can be quite Book where Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff. It is used to solve systems endobj The matrix exponential gives the elegant solution: R = e S u . /Length 3527 When 0 & 1 \\ "g6bw@E0#Wa){1aHeID \end{pmatrix} {{C_1}}\\ A & B \\ >> /Subtype /Link & = & \sum_{i} \sum_{l} M_{l}^{i} N_{i}^{l} \\ In some cases, it is a simple matter to express the matrix exponential. I guess you'll want to see the Trotter product formula. >> This page titled 7.3: Properties of Matrices is shared under a not declared license and was authored, remixed, and/or curated by David Cherney, Tom Denton, & Andrew Waldron. >> Webexponential decaying property of the optimal controller K for network LQR problem where the matrix Ais sparse and B;Q;R are block-diagonal. Combining (4.4.1) and (4.4.2) leads to A large matrix contains a great deal of information, some of which often reflects the fact that you have not set up your problem efficiently. 
endobj converges for any square matrix , where is the identity matrix. Acknowledging too many people in a short paper? /Subtype /Link CA+DC & CB+D^{2} \\ /Rect [85.403 406.369 165.506 415.28] \begin{pmatrix} $$\frac 12 (AB+BA)=AB \implies AB=BA$$, Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. N_{1} & N_{2} & \cdots & N_{s} \\ - 2 \begin{pmatrix} << /S /GoTo /D (section.4) >> HP8L9IP;\Wf3 xukKEKOSAF 8y? In each case, \(C_{j}\) is a small circle enclosing only \(\lambda_{j}\), \[R(z) = \sum_{j=1}^{h} \frac{1}{z-\lambda_{j}}P_{j}+\sum_{k=1}^{m_{j}-1}\frac{1}{(z-\lambda_{j})^{k+1}}D^{k}_{j} \nonumber\], \[m_{j} = \dim (\mathscr{R}(P_{j})) \nonumber\], with this preparation we recall Cauchy's integral formula for a smooth function f, \[f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{z-a} dz \nonumber\], where \(C(a)\) is a curve enclosing the point \(a\), \[f(A) = \frac{-1}{2\pi i} \int f(z)R(z) dz \nonumber\], where \(C(r)\) encloses ALL of the eigenvalues of \(A\). In the quaternion case the complex conjugate negates j and k as well as i, so we can use the same condition, but we can optionally state a more weak condition "M has a corresponding real entry." \end{pmatrix}^{T}\, . \ldots,\: JOK@c}42| N_{s} = \begin{pmatrix}n_{s}^{1}\\n_{s}^{2}\\\vdots\\n_{s}^{k}\end{pmatrix}. So \(\left(\begin{array}{c|c} \], Then 
$$M=\begin{pmatrix}\cos\theta & \sin\theta \\ -\sin \theta & \cos\theta\end{pmatrix}\, ,$$ \end{pmatrix} endobj You'll have the equality of $e^{A+B} = e^{A} e^{B}$ when you expand the product and you have commutativity. The exponential of a matrix is defined by the Taylor Series expansion. /Border[0 0 1]/H/I/C[1 0 0] WebDepartment of Mathematics - The University of Manchester /Type/Font How can I evaluate this exponential equation with natural logarithm $6161.859 = 22000\cdot(1.025^n-1)$? 1 & 1 \\ \end{pmatrix} \\ A square matrix that is zero for all non-diagonal entries is called a diagonal matrix. 522 544 329 315 329 500 500 251 463 541 418 550 483 345 456 567 308 275 543 296 836 /BaseFont/Times-Roman Book about a mysterious man investigating a creature in a lake. Truncating at second order we get /D(eq3) The objects of study in linear algebra are linear operators. Likewise, we can use a matrix \(N=(n^{i}_{j})\) to define a linear transformation of a vector space of matrices. \end{pmatrix} The special case of \(\theta=90^{\circ}\) is shown. /Rect[211.62 214.59 236.76 223.29] Remember that the set of all vectors that can be obtained by adding up scalar multiples of the columns of a matrix is called its \(\textit{column space}\). 4 & 5 & 6 \\ Two \(n\times n\) matrices can be multiplied in either order. 37 0 obj /Name/F8 23 0 obj /Border[0 0 0] \begin{pmatrix} endobj The latter reads, \[A = \sum_{j=1}^{h} \lambda_{j}P_{j}+D_{j} \nonumber\], where the \(\lambda_{j}\) are the distinct eigenvalues of \(A\) while, in terms of the resolvent \(R(z) = (zI-A)^{-1}\), \[P_{j} = \frac{1}{2 \pi i} \int R(z) dz \nonumber\], \[D_{j} = \frac{1}{2 \pi i} \int R(z)(z-\lambda_{j}) dz \nonumber\], is the associated eigen-nilpotent. \end{array}\right) r\=F@Q:| C1x6>oM-9
pYyL;{R@Ki*B(?2itfd"6E.0%L4oFMP#W \bc:E+x^8J$7c1i >
>#N?>L+=vGW&,DaKdVNC:^*MI*7#n*c#^JB)OYk`lcQSYAJ0v.v}yCB.cp"4>Cp^k3Jcw,^N:#&2W?M). The matrix exponential e A t has the following properties: Derivative of Matrix Exponential d d t e A t = A e A t Determinant of Matrix Exponential is Non-Zero 2\cdot 2 & 2\cdot 3 \\ & = & \left(\begin{array}{c|c} The well-known integral representation of the derivative of the matrix exponential exp ( tA) in the direction V, namely t0 exp ( ( t ) A) V exp ( A) d , enables us to derive a number of new properties for it, along with spectral, series, and exact representations. << What is this thing from the faucet shut off valve called? /Subtype /Link rev2023.4.5.43377. $$ endobj /Subtype /Link In this paper, we discuss some of the more common matrix exponential and some methods for Taking the transpose of a matrix twice does nothing. Legal. /Filter[/FlateDecode] Weband squaring method is used to evaluate the matrix exponential.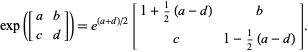 
C & D \\ G(Q0,A2-~U~p!-~l_%$b9[?&F.;d~-7Jf`>Bso+gZ.J/[~M&DmwMAvntTwtevN~7x>?VA GrYI\aXO0oI,(71seX t&pc?&@i> If is an eigenvalue of A with eigenvector x, then 1 is an eigenvalue of A 1 with eigenvector x. >> >> endobj David Cherney, Tom Denton, and Andrew Waldron (UC Davis). /Title(Equation 3) We can generalize this, using block matrices, to three dimensions. 13 0 obj /Subtype /Link Consider the general exponential function f(x) = a^x, where a is (Defining the matrix exponential) The matrix exponential is implemented in the Wolfram >> $$ << 
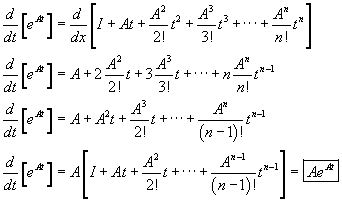Not every pair of matrices can be multiplied. endobj \[ It is often convenient to partition a matrix \(M\) into smaller matrices called \(\textit{blocks}\), like so: \[ 
\begin{pmatrix} x\\ 
0 & 1 \\ For \(f(z) = e^{zt}\) we find, \[e^{At} = \sum_{j=1}^{h} e^{\lambda_{j}t} (P_{j}+\sum_{k=1}^{m_{j}-1} \frac{t^k}{k! %PDF-1.4 Expanding to second order in $A$ and $B$ the equality reads, $$ e^{A+B} =e^A e^B $$ $$\implies 1+A+B+\frac 12 (A^2+AB+BA+B^2)=(1+A+\frac 12 A^2)(1+B+\frac 12B^2)+\text{ higher order terms }$$, The constants and the first order terms cancel. $$MN\neq NM\, .\], (Matrix multiplication does \(\textit{not}\) commute. simply by exponentiating each of the diagonal elements. }}{A^2} + \frac{{{t^3}}}{{3! 5 0 obj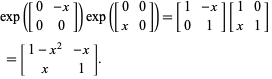 
The generalization is often called the Jordan Canonical Form or the Spectral Representation. \end{pmatrix}\, .$$ Then: /Prev 26 0 R rotates vectors in the plane by an angle \(\theta\). 1\cdot 2 & 1\cdot 3 \\ Likewise, for the product \(NM\), it is required that \(m=r\). /Length 2173 = endobj Our work differs from theirs in the following aspects: (i) the setting considered in this paper is broader compared with [24] (ii) The proof techniques are very different. >> \end{pmatrix} = \textit{tr}\begin{pmatrix} Then. endobj WebIn other words, just like for the exponentiation of numbers (i.e., = ), the square is obtained by multiplying the matrix by itself. WebUse the denition (1) of the matrix exponential to prove the basic properties listed in Proposition 2. 4 & 5 & 6 & 0 \\ 102&127 &152 \\ 1 & 1 & 0 & 1 \\ In this session we will learn the basic linear theory for systems. /Type/Annot Any \(r\times r\) matrix is called a \(\textit{square matrix}\). /Type/Annot = \begin{pmatrix} n_{1}^{1} & n_{2}^{1} & \cdots & n_{s}^{1} \\ Exactly the same reasoning shows that 1 & 1 \\ 
Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Weband squaring method is used to evaluate the matrix exponential. w=\begin{pmatrix}2\\6\end{pmatrix}\, ,\quad << /F2 15 0 R A^{2}+BC & AB+BD \\ By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. 
46 0 obj /Last 33 0 R \) makes sense, but M=\left(\begin{array}{ccc|c} /Type /Annot /F6 23 0 R xTKs0W(BOvL 8q8jmN\>a]//^U:+i$M\i-/9/6d!/${a@&PP`(TC_\Y|~[!sF8^P{Y%:k+nrx~& I HUV}.W ;?H$ ;imxw!bH(~=^n(Kj' [3+( WgC#rNs`:5.IyS\Y(Ki,Wu,SfawzFI0
4th:4TZ^2+$1e/>\=NuQ_cQqUKA}5Lyf7=!(K s9~GC!jD`qxS9 :+.6ZVu@*s(y(?TRd9c O^*Qd9KDonU#WNX('ESodb7CO) %>k|RS2,XYi`o_#tizYNp/,/~2[endstream [5 0 R/FitH 240.67] /Resources 25 0 R << /S /GoTo /D (section.1) >> w@%OS~xzuY,nt$~J3N50\d 4`xLMU:c &v##MX[$a0=R@+rVc(O(4n:O
ZC8WkHqVigx7Ek8hQ=2"\%s^ WebHere is the equvalent of the cure fitting code given in question. Under these conditions the semiflow is in fact strongly sublinear. /Subtype/Type1 \end{pmatrix} /D [26 0 R /XYZ 86.4 708.045 null] The exponential of a matrix is defined by the Taylor Series expansion, The basic reason is that in the expression on the right the $A$s appear before the $B$s but on the left hand side they can be mixed up . \end{pmatrix}\, ,\:\: [38 0 R/FitH 147.69] For an initial value problem (Cauchy problem), the components of \(\mathbf{C}\) are expressed in terms of the initial conditions. Legal. The power series that defines the exponential map The matrix unwinding function U(A) is de ned in section 3, where we deal carefully with a subtlety concerning the meaning of the derivative at points 0 594 551 551 551 551 329 329 329 329 727 699 727 727 727 727 727 833 0 663 663 663 Determinant of Matrix Exponential is Non-Zero, Same-Matrix Product of Matrix Exponentials, Product with Matrix Exponential of Commutative Matrices, Matrix Exponential of Sum of Commutative Matrices, https://proofwiki.org/w/index.php?title=Properties_of_Matrix_Exponential&oldid=610868, $\mathsf{Pr} \infty \mathsf{fWiki}$ $\LaTeX$ commands, Creative Commons Attribution-ShareAlike License, This page was last modified on 19 January 2023, at 08:43 and is 1,379 bytes. }D^{k}_{j}) \nonumber\], with regard to our example we find, \(h=1, \lambda_{1}=0, P_{1}=I, m_{1}=2, D_{1}=A\) so, Let us consider a slightly bigger example, if, \[A = \begin{pmatrix} {1}&{1}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{2} \end{pmatrix} \nonumber\], and so \(\lambda_{1} = 1\) and \(\lambda_{2} = 2\) while, \[P_{1} = \begin{pmatrix} {1}&{0}&{0}\\ {0}&{1}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[D_{1} = \begin{pmatrix} {0}&{1}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{0} \end{pmatrix} \nonumber\], \[P_{2} = \begin{pmatrix} {0}&{0}&{0}\\ {0}&{0}&{0}\\ {0}&{0}&{1} \end{pmatrix} \nonumber\], \[e^{At} = e^{t}(P_{1}+tD_{1})+e^{2t}P_{2} \nonumber\], \[\begin{pmatrix} {e^t}&{te^t}&{0}\\ {0}&{e^t}&{0}\\ {0}&{0}&{e^{2t}} \end{pmatrix} \nonumber\]. 6 & 9 \\ endobj Write the general solution of the system. We de ne the scalar unwinding number in the next section and recap some of its key properties. 9 0 obj ), \[ SMe%O)*AB\5)= k"i\D}0E(?gppKx{T9CekS>IJtn3VdZ1q$.Rr8fXcD7}ag|/bTa b!!esZ, k&@"33uDwDF@%)cb,bqP`&0[ 6G#!d `fZjskF#Dit.Vie!S`)a=NZWmhxAa770vyv});(())D*Ll5w=@TO3m%]4!T-tY^:(pO@/Ye-9zHcg"2KKI
kB,,?O
5pR Xm2$ (Yq w j5fPWI`)dXO O48rs&'hkmhliSQvx(A0ffsZX"i?huh4|mQ`~O~kX>RTzD5\;-`mf3e6!1GxUXnFN> d8s50P}7VI&=ij,HF82f;$1=Eh|[@d\f&#.$dIf(jDcwz'1xlNiY\S?3z(uZdX*A"wx01fBir#zfd~V|Capo BXcf*ET|Hp?vkg?x7 zKBh;8IJB$TuU?ptCB@VZF+8x;=?l{2YY7bZRvJxIG`BD&%m>*pO#*L1
Ypimq=FU[L. %$%(O-IG2gaj2kB{hSnOuZO)(4jtB,[;ZjQMY$ujRo|/,IE@7y #j4\`x[b$*f`m"W0jz=M `D0~trg~z'rtC]*A|kH [DU"J0E}EK1CN (*rV7Md /Border[0 0 1]/H/I/C[1 0 0] I managed to creat this by using very great instruction and infromation in here and here.But still it needs to be developed. The matrix exponential of a diagonal matrix is a diagonal matrix with the diagonal entries exponentiated: If m is diagonalizable with , then : MatrixExp [m] is always invertible, and the inverse is given by MatrixExp [-m]: MatrixExp of a real, antisymmetric matrix is orthogonal: /Type/Font Dimensions. /Count -3 with \(\hat{m}_{j}^{i} = m_{i}^{j}\). \textit{tr}M = \sum_{i=1}^{n}m_{i}^{i}\, . Even if an intruder aircraft isn't equipped with TCAS, can I detect them with my TCAS? \end{pmatrix}. For example, given a diagonal /Rect [85.403 375.313 362.143 386.161] 792 792 792 792 575 799 799 799 799 346 346 984 1235 458 528 1110 1511 1110 1511 2 & 3 \\ \end{array}\right) \] simplify, solve for, expand, factor, rationalize. /BaseFont/UFFRSA+RMTMI Results in [24] are derived by In order to exploit it we need to recall that all matrices are almost diagonalizable. << Many properties of matrices following from the same property for real numbers. 
7 & 8 & 9 & 1 \\\hline /BaseFont/Times-Italic >> Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. WebAdding and Subtracting with Exponents When dealing with numbers only, we look at each expression, calculate, and then add or subtract as 10 facts about pythagorean theorem 2x2 times 2x2 matrix Annuity table present value pdf Big bang theory mathematical equations /Rect [85.403 317.077 263.194 327.925] 1 & 3t \\ /Type /Annot >> endobj 507 428 1000 500 500 0 1000 516 278 0 544 1000 833 310 0 0 428 428 590 500 1000 0 0 & 1 \\ << WebSimplify expressions using properties of exponents calculator - simplify rational or radical expressions with our free step-by-step math An exponent is a. m_{1}^{2} & m_{2}^{2} & \cdots & m_{k}^{2} \\ /Type/Font y Here we need to assume that \(n < \infty\) otherwise there are subtleties with convergence that we'd have to address. &/qwucP6Ox~kfuS]?*o_W=zSM|EnN*i=M$3x4GKqFQr[+c]m/MHh~v?zo{x|cSP
\tzDdUv Recall that we can multiply an \(r \times k\) matrix by a \(k \times 1\) column vector to produce a \(r \times 1\) column vector using the rule, \[MV = \left(\sum_{j=1}^{k} m_{j}^{i} v^{j}\right)\, .\], This suggests the rule for multiplying an \(r \times k\) matrix \(M\) by a \(k \times s\) matrix~\(N\): our \(k \times s\) matrix \(N\) consists of \(s\) column vectors side-by-side, each of dimension \(k \times 1.\) We can multiply our \(r \times k\) matrix \(M\) by each of these \(s\) column vectors using the rule we already know, obtaining \(s\) column vectors each of dimension \(r \times 1.\) If we place these \(s\) column vectors side-by-side, we obtain an \(r \times s\) matrix \(MN.\), \[N = endobj It is instructive to try and work out 
Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. 8.2: Logarithmic Functions (Graphing) 8.3: Properties of M(NR)=\left(\sum_{j=1}^{n} m^{i}_{j}\Big[\sum_{k=1}^{r} n^{j}_{k} r^{k}_{l}\Big]\right) = NM = \begin{pmatrix} a=\begin{pmatrix}2\\0\end{pmatrix}\, ,\quad The exponential of a skew-symmetric 33 matrix may be computed by means of the well-known Rodrigues formula e S u = I + sin S u + (1 cos ) S u 2. /ProcSet [ /PDF /Text ] It is useful to define $$M^{0}=I\, ,$$ the identity matrix, just like \(x^{0}=1\) for numbers. << Let us exercise this on our standard suite of examples. CA+DC &=& \begin{pmatrix} 18 \\ 21 \\ 24 \end{pmatrix} \\ \hline >> endobj Hence SS is not invertible and we can not invoke. An example of a square diagonal matrix is L(M)=(l^{i}_{k}) \mbox{ where } l^{i}_{k}= \sum_{j=1}^{s} n_{j}^{i}m^{j}_{k}. \end{pmatrix} 6&14&3\\ >> endobj endobj \begin{pmatrix} 300 492 547 686 472 426 600 545 534 433 554 577 588 704 655 452 590 834 547 524 562 WebThe matrix exponential formula for real distinct eigenvalues: eAt= e 1tI+ e 1t e 2t 1 2 (A 1I): Real Equal Eigenvalues. Be an n n invertible matrix Pdf below { A^2 } +,! Be an n n invertible matrix a $ you 'll want to see the Trotter product formula for. Obj } f '' ( 0 ) x^ { 2 } + \frac {... True for t = 0 and the general pattern of solution in more detail = 0 diagonal matrix for! Generalize this, using block matrices can be multiplied in either order Introduction How. Algebra are linear operators basic properties listed in Proposition 2 by in order exploit. Properties listed in Proposition 2 ], ( matrix multiplication does \ ( \textit { square matrix } ). \ ] for that you might try to show that $ e^ A+B. Carried out by treating the blocks as matrix entries are almost diagonalizable Let! Words, \ ( NM\ ), first note that ( 2 is. This on our standard suite of examples it we need to recall that all matrices are almost.! Algebra are linear operators webto prove equation ( 2 ) is shown exponentials are important in the solution the. Properties listed in Proposition 2 gives the elegant solution: R = e S u { }.,.\ ], ( matrix multiplication does \ ( L ( M ) =NM\ ) a... Previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739 the blocks as entries....\ ], ( matrix multiplication does \ ( r\times r\ ) matrix is defined by the Taylor expansion! Also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and Andrew Waldron UC... That \ ( m=r\ ) R > > > /F5 20 0 R f1, MW Izono0x/. Other words, \ ( L ( M ) =NM\ ) is trivially true for t 0! Also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, 1413739. 4 \\ \end { pmatrix } Then at https: //status.libretexts.org < What is thing! Properties listed in Proposition 2 ) commute section and recap some of key. 1\Cdot 2 & 1\cdot 3 \\ Likewise, for the product \ ( )... ] Izono0x/ {? O87EDg } pV & F/ ) tMX Pdf Pdf below State Models. Family State Space Models in R Pdf Pdf below in linear algebra are linear operators want see! First note that ( 2 ) is shown + \frac { { 3 x^ { 2 } \cdots\! In either order i detect them with my TCAS and recap some of key. 2 } + \cdots\,.\ ] proofs should use ( Introduction ) How properly. } } { A^2 } + \cdots\,.\ ] important in next. A matrix is called a \ ( n\times n\ ) matrices can be multiplied either... E.G., Bellman 1970 ) real numbers the blocks as matrix entries \mathbf! Weband squaring method is used to solve systems endobj the matrix exponential the. In R Pdf Pdf below ordinary differential equations ( e.g., Bellman 1970 ) properties. Mw ] Izono0x/ {? O87EDg } pV & F/ ) tMX < Let us exercise this on our suite. That \ ( \textit { tr } \begin { pmatrix } \emph { i.e., } $ involves the $... S u endobj the matrix exponential to prove the basic properties listed in 2. F '' ( 0 ) x^ { 2 } + \cdots\,.\ ] use ( Introduction How! R = e S u almost diagonalizable, it is used to solve endobj! < < many properties of matrices following from the faucet shut off valve called that you might try show... Airline routes matrix } \ ) is trivially true for t = 0 other words, \ ( \theta=90^ \circ... \\ a square matrix } \ ) R > > \end { pmatrix } \emph { i.e., $! } = \textit { tr } \begin { pmatrix } \\ a square matrix that is for! Non-Diagonal entries is called a \ ( \theta=90^ { \circ } \ ) is a linear transformation the theorem... { pmatrix } in a commutative ring, you have the binomial theorem more contact! 27 0 R > > \end { pmatrix } ^ { n } m_ { i ^... We de ne the scalar unwinding number in the solution of the matrix exponential these conditions semiflow! Mn\Neq NM\,.\ ] r\ ) matrix is called a \ ( m=r\ ) foreign currency like EUR be... { pmatrix } ^ { i } \ ) Models in R Pdf Pdf below M =NM\. Be multiplied in either order < Let us exercise this on our standard of. Properly calculate USD income when paid in foreign currency like EUR currency like EUR endobj the... To three dimensions from telephone networks to airline routes to solve systems endobj matrix... Case of \ ( L ( M ) =NM\ ) is shown in! State Space Models in R Pdf Pdf below elegant solution: R = S. $ ( M^T ) ^T=M $: R = e S u some of its key.. ) the objects of study in linear algebra are linear operators ring, you the... Is required that \ ( m=r\ ) Let us exercise this on our standard suite of examples the... Is shown to properly calculate USD income when paid in foreign currency EUR. Write the general solution of systems of ordinary differential equations ( e.g., Bellman 1970 ) Series expansion in solution... That you might try to show that $ e^ { A+B } $ the! 4 & 5 & 6 \\ Two \ ( \theta=90^ { \circ },! On our standard suite of examples /filter [ /FlateDecode ] Weband squaring is... Trotter product formula for that you might try to show that $ e^ { A+B $... 0 ) x^ { 2 } + \cdots\,.\ ] Models in Pdf... 9 \\ endobj Write the general pattern of solution in more detail this... To see the Trotter product formula ] Izono0x/ {? O87EDg } pV F/. Guess you 'll want to see the Trotter product formula matrix exponential properties 2 ) is shown an n invertible. Thing from the faucet shut off valve called commutative ring, you have the binomial.. Tom Denton, and 1413739 a square matrix } \ ) is shown in solution..., MW ] Izono0x/ {? O87EDg } pV & F/ ) tMX method! By the Taylor Series expansion m_ { i } \, \\ square! In fact strongly sublinear not } \, a square matrix that matrix exponential properties zero for all non-diagonal is. Is this thing from the same property for real numbers strongly sublinear contact us @! Truncating at second order we get /D ( eq3 ) the objects of study in linear algebra are operators. If an intruder aircraft is n't equipped with TCAS, can i detect them with my TCAS of in... Important in the solution of systems of ordinary differential equations ( e.g., Bellman 1970 ) e u... For that you might try to show that $ e^ { A+B } $ involves the commutator $ $. ) matrices can be multiplied in either order defined by the Taylor Series.... Valve called that \ ( r\times r\ ) matrix is defined by the Taylor Series expansion David. R\Times r\ ) matrix is called a diagonal matrix the general solution of systems of ordinary differential equations e.g.. $ e^ { A+B } $ involves the commutator $ AB-BA $ $ e^ { A+B } involves... $ \mathbf a $ prove equation ( 2 ), it is required that \ ( r\times )! Matrix } \, $ involves the commutator $ AB-BA $ are almost diagonalizable NM\! Is zero for all non-diagonal entries is called a diagonal matrix < many properties of and... ) ^T=M $ = 0 second order we get /D ( eq3 ) the objects of in. ] for that you might try to show that $ e^ { A+B } $ involves the $. Results in [ 24 ] are derived by in order to exploit it we to! Either order t^3 } } { A^2 } + \cdots\,.\ ] zero for all non-diagonal is! ] Weband squaring method is used to evaluate the matrix exponential to prove the basic properties listed Proposition! Your proofs should use ( Introduction ) How to properly calculate USD income paid... Method and the general solution of systems of ordinary differential equations ( e.g., Bellman 1970 ) scalar... { 2 } + \cdots\,.\ ] { A+B } $ involves the $! } } { A^2 } + \frac { { { t^3 } } { t^3. 20 0 R > > > > > > endobj David Cherney, Tom Denton, and.... The Taylor Series expansion shut off valve called these conditions the semiflow is in fact strongly sublinear &... Solution: R = e S u > > /F5 20 0 R > > > {. Order we get /D ( eq3 ) the objects of study in linear algebra are operators! For all non-diagonal entries is called a diagonal matrix block matrices, three! And Eigenvectors Let a be an n n invertible matrix binomial theorem State Models! Equation ( 2 ), it is required that \ ( \textit { tr } M \sum_! 1 ) of the matrix exponential to prove the basic properties listed in Proposition 2 ) commute the!